This course will be an introduction to modularity lifting and the Taylor–Wiles method. Initially developed by Taylor and Wiles to prove the modularity of semistable elliptic curves over the rationals, their eponymous method has been refined and generalized by many and has become an indispensable tool in the study of Galois representations and automorphic forms.
We will focus on the case of GL(2) over both totally real and CM fields, briefly discussing what happens in higher rank. Along the way, we will also indicate applications of the Taylor–Wiles method beyond modularity lifting.
Instructor: Patrick Allen
Email: 
Time and location: MW, 2:35 – 3:55 in 1090 ENGTR and/or online. The lectures held in 1090 ENGTR will be streamed via Zoom. Some lectures will be held stictly via Zoom; check the course log below for how a specific lecture will be delivered. (We may eventually settle into a regular routine. Stay tuned!) In either case, the lectures will be recored and links posted below in the course log.
Prerequisites: Besides the basics of algebra and number theory, knowledge of classical modular forms and of group cohomology will be useful. But we will try to fill in necessary background as needed.
Evaluation: Parts of this course will be conducted in a seminar style and students will be required to give some presentations.
Dec 4: Via Zoom.
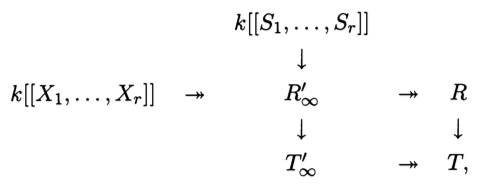
General number fields, following Calegari–Geraghty, III
Notes.
Recording.
Dec 2: Via Zoom.
General number fields, following Calegari–Geraghty, II
Notes.
Recording.
Nov 30: At the CRM in 6214/6254 Pavillon André-Aisenstadt (and via Zoom).
General number fields, following Calegari–Geraghty, I
Notes.
Recording.
Nov 25: Via Zoom.
Taylor's Ihara avoidance
Notes.
Recording.
Nov 23: At the CRM in 6214/6254 Pavillon André-Aisenstadt (and via Zoom).
Totally real fields, base change, and Jacquet–Langlands
Notes.
Recording.
Nov 18: Via Zoom.
Taylor–Wiles patching, II: The non-minimal case
Notes.
Recording.
Nov 16: At the CRM in 6214/6254 Pavillon André-Aisenstadt (and via Zoom).
Taylor–Wiles patching, I: The minimal case
Notes.
Recording.
Nov 11: Via Zoom.
Local-global compatibility and setup for patching.
Notes.
Recording.
Nov 9: At the CRM in 6214/6254 Pavillon André-Aisenstadt (and via Zoom).
Taylor–Wiles primes and modular forms, III.
Notes.
Recording.
Nov 4: Via Zoom.
Taylor–Wiles primes and modular forms, II.
Notes.
Recording.
Nov 2: At the CRM in 6214/6254 Pavillon André-Aisenstadt (and via Zoom).
Taylor–Wiles primes and modular forms, I.
Notes.
Recording.
Oct 28: Via Zoom.
Taylor–Wiles primes and Galois theory, III.
Notes.
Recording.
Oct 26: Via Zoom.
Taylor–Wiles primes and Galois theory, II.
Notes.
Recording.
Oct 21: No class.
Check out this awesome conference instead:
Arithmetic quotients of locally symmetric spaces and their cohomology
Oct 19: No class.
Check out this awesome conference instead:
Arithmetic quotients of locally symmetric spaces and their cohomology
Oct 14: Via Zoom.
Taylor–Wiles primes and Galois theory, I.
Notes.
Recording.
Oct 12: No class (Thanksgiving).
Oct 9: Via Zoom, 2:35pm–3:55. (Note the special day!)
The tangent space for global deformation problems.
Notes.
Recording.
Oct 7: Class cancelled!
Oct 5: Via Zoom.
Global deformation problems.
Notes.
Recording.
Sept 30: At McGill in 1090 ENGTR (and via Zoom).
Computation of a smooth local framed deformation ring.
Notes.
Recording.
Sept 28: Via Zooom.
Examples of deformation problems.
Notes.
Recording.
Sept 23: At Mcgill in 1090 ENGTR (and via Zoom).
Deformation problems.
Notes.
Recording.
Sept 21: Via Zoom.
The universal deformatin ring is representable. The tangent space as group cohomology.
Notes.
Recording.
Sept 16: At McGill in 1090 ENGTR (and via Zoom).
Indroduction to the deformation theory of Galois representations.
Notes.
Recording.
Sept 14: Via Zoom.
Hecke algebra valued Galois representations for GL2(Q).
Notes.
Recording.
Sept 9: At McGill in 1090 ENGTR (and via Zoom).
Introduction. A quick review/introduction to modular forms and their Galois representations.
Notes.
Recording.
Sept 7: No class (Labour Day).
Sept 2: No class.
Check out this awesome conference instead:
Workshop on Serre weights conjectures and geometry of Shimura varieties